Para comenzar el año vemos el calendario matemático para 2014
Enero 2014
Febrero 2014
Marzo 2014
Abril 2014
Mayo 2014
Junio 2014
Vamos a comenzar con dos juegos:
Los números
Diffy
DECIMALES
Convertir Fracciones a Decimales
El método más simple es usar una calculadora.
 | ¡Nada más divide el numerador (la parte de arriba de la fracción) por el denominador (la de abajo) y lee la respuesta! |
Ejemplo: ¿Cuánto es 5/8 como fracción? | |
... toma tu calculadora y pon "5 / 8 =", la respuesta debe ser 0,625 |
Convertir Decimales a Fracciones
Para convertir un Decimal a una Fracción sigue estos pasos:
| Paso 1: Escribe el decimal dividido por 1. |
| Paso 2: Multiplica el numerador y denominador, por 10 una vez por cada decimal luego de la coma. (Por ejemplo, si hay dos números luego del decimal, multiplícalos por 100, si hay tres usa el 1000, etc.) |
| Paso 3: Simplifica (reduce) la fracción |
Ejemplo 1: Expresar 0.75 como fracción
Paso 1: Escribe:
| 0.75 |
| 1 |
| × 100 | ||
 | ||
| 0.75 | = | 75 |
| 1 | 100 | |
 | ||
| × 100 | ||
(¿Ves como el numerador se convierte en un entero?)Paso 3: Simplifica la fracción:
| ÷ 25 | ||
| ||
| 75 | = | 3 |
| 100 | 4 | |
| ||
| ÷ 25 | ||
Respuesta = 3/4
Nota: ¡75/100 se llama una fracción decimal y
3/4 es llamada una fracción común !
Ejemplo 2: Expresa 0.625 como una fracción
Paso 1: escribe:
| 0.625 |
| 1 |
Paso 2: multiplica el número de arriba y el de abajo por 1.000 (había 3 dígitos luego de la coma así que es 10×10×10=1.000)
| 625 |
| 1.000 |
Paso 3: simplifica la fracción (me llevó dos pasos aquí):
| ÷ 25 | ÷ 5 | |||
| | ||||
| 625 | = | 25 | = | 5 |
| 1.000 | 40 | 8 | ||
| | ||||
| ÷ 25 | ÷ 5 | |||
Respuesta = 5/8
Ejemplo 3: Expresa 0.333 como fracción
Paso 1: Escribe abajo:
| 0.333 |
| 1 |
| 333 |
| 1000 |
¡No se puede simplificar!
Respuesta = 333/1000
Pero una Nota Especial:
Si en realidad quieres expresar 0,333... (en otras palabras los 3 repitiéndose para siempre lo que se llama 3 periódico) entonces necesitas seguir un argumento especial. En este caso escribimos:
| 0,333... |
| 1 |
Y entonces MULTIPLICAMOS ambos lados por 3:
| × 3 | ||
| ||
| 0.333... | = | 0.999... |
| 1 | 3 | |
| ||
| × 3 | ||
Y 0.999... = 1 (¿Es así? - Esta historia te lo demuestra), así que:
Respuesta = 1/3
Pequeña historia
Hace unos días, Leonhard puso en su perfil de Facebook una pregunta matemática que dividió a los economistas y actuarios que los tenemos de amigo (amigo en Facebook, que se entienda; porque después el tipo se agranda y se cree que cae simpático a una multitud).
La pregunta es la que da título a este post.
¿0,9 periódico es igual a 1?
Rápidamente, los economistas y actuarios dijimos, unánimemente y a coro: “¡Noooooooo! ¡Son dos números distintos!”.
Bueno, Leonhard nos mandó esta demostración y nos quemó los papeles:
1 = 3 / 3 = 3 x (1/3) = 3 x 0,3 periódico = 0,9 periódico
Q.E.D.
Como se imaginarán, se abrieron las aguas de la unanimidad y empezamos a pelearnos todos, a favor y en contra de la demostración. El combate sigue arduamente, como tipos tozudos que nos preciamos de tal, pero dio motivo a este post.
Efectivamente, 0,9 periódico (esto es, 0,99999999… infinitos nueves) es igual a 1. Ambas expresiones son idénticos modos de representar la unidad.
Hay un muy buen artículo en Wikipedia, porque expone varias demostraciones de esta igualdad (ya probada en 1770 por Leonhard Euler):
El periódico 0,999
DECIMALESDefinición de decimal
Cómo entender los números decimales...... como un número entero más décimas, centésimas, etc.
Puedes pensar que un número decimal es un número entero más décimas, centésimas, etc.:
Ejemplo 1: ¿ Qué es 2,3 ?
Ejemplo 2: ¿ Qué es 13,76 ?
... como una fracción decimal
O puedes entender un número decimal como una fracción decimal.
... como un número entero y una fracción decimal
O puedes pensar en un número decimal como un número entero más una fracción decimal.
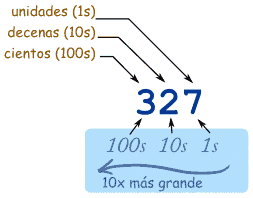
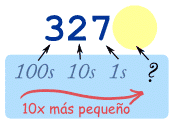
En el número 327:
... y ...
¡Y eso es un número decimal!
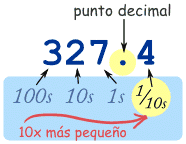
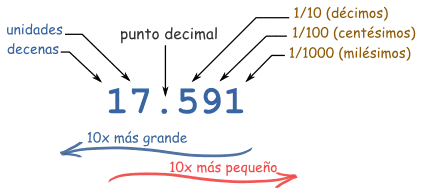
Punto decimal
El punto decimal es la parte más importante de un número decimal. Está exactamente a la derecha de la posición de las unidades. Sin él, estaríamos perdidos y no sabríamos cuál es cada posición.
Ahora podemos seguir con valores más y más pequeños, como décimas, centésimas, y más, como en este ejemplo:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||
Tomemos un rectángulo del tamaño que deseemos. Sea del tamaño que sea, diremos que tiene tamaño unidad, su longitud será de 1 unidad y será el que está dibujado de color rojo.
Si tomamos ese cuadrado y lo divido en 10 partes iguales y tomo la primera, obtendré el rectángulo azul. Este rectángulo será la décima parte del anterior. Si tomo este último rectángulo y, a su vez, lo divido en otras 10 partes tendré 0,1 veces el azul, o sea, 0,01 veces el rojo.
Definición:
 | La décima, la centésima son unidades decimales. También lo son la milésima (m), la diezmilésima, etc.
|
- Descomposición de un número decimal
Un número decimal se puede descomponer de varias formas, como se muestra en esta tabla:
| Número | Descomposición | Lectura |
| 2,375 2,375 2,375 | 2 + 0,3 + 0,07 + 0,005 2 + 0,375 2 + 0,37 + 0,005 | 2 unidades, 3 décimas, 7 centésimas y 5 milésimas. 2 unidades y 375 milésimas. 2 unidades, 37 centésimas y 5 milésimas. |
- Suma de números decimales
Vamos a sumar dos números decimales: 5,7 y 1,8.
Para ello, usaremos dos métodos uno gráfico y otro más matemático.
Si el 5,7 fuese una barra de dicha longitud podría representarse como:
de la misma forma, representamos una barra de 1,8 metros:
Para hallar la longitud de la b arra resultante hay que sumar 5,7 m y 1,8 m,
para ello unimos las dos barras como muestra la figura::
La longitud de la barra es 7,5 metros.
Definición:
| P ara sumar números decimales:
|
- Resta de números decimales.
Para restar dos números decimales imaginaremos que de una barra que mide 5,7 m, se corta un trozo de 1,8 m.
Para hallar la longitud del otro trozo hay que restar 5,7 m y 1,8 m:
Matemáticamente:
5,7-1,8=3,9.
La longitud del otro trozo es 3,9 m.
Definición:
| Para restar dos números decimales:
|
Multiplicación y división de decimales por potencias de 10
Al multiplicar decimales por una potencia de 10, debemos correr la coma del decimal a la derecha según cuantos ceros tenga la potencia de 10 y al dividir decimales por potencias de 10, debemos seguir el mismo procedimiento, pero esta vez la coma la debemos correr hacia la izquierda.
Ejemplo:
Cuando al multiplicar, la potencia de 10 tiene más ceros que las cifras decimales del otro factor, debemos agregar cuantos ceros sean necesarios después de la última cifra decimal.
En el caso de las divisiones en que la potencia tenga más ceros que las cifras enteras del otro factor, debemos anteponer cuantos ceros sean necesarios a la izquierda de la parte entera del decimal.
En el caso de las divisiones en que la potencia tenga más ceros que las cifras enteras del otro factor, debemos anteponer cuantos ceros sean necesarios a la izquierda de la parte entera del decimal.
Así:
2) Multiplicación y división de decimales
Al multiplicar dos números decimales debemos seguir el mismo procedimiento que utilizamos al multiplicar dos números naturales como muestra la siguiente figura:
Luego contaremos cuantos dígitos hay después de la coma en ambos factores. Ojo que no deben contabilizarse ceros que estén después del último dígito de la parte decimal. Luego debemos poner la coma esa cantidad de espacios partiendo desde el último dígito del producto, es decir, de derecha a izquierda.
Como tenemos 3 dígitos después de la coma entre los dos factores, debemos poner la coma en el producto como se muestra a continuación:
En el caso de la división debemos multiplicar tanto el dividendo como el divisor por la misma potencia de 10 que sea necesario para que ambos decimales queden expresados como números decimales con período cero, es decir, como números naturales. Luego debemos dividir como lo hacemos con dos números naturales.
Veamos un ejemplo:
Página de divisiones de decimales AQUÍ
Juego del KENKEN Para empezar con los más sencillos AQUÍ
¿Sabes cuadrar dos círculos? Se hace ASÍ
Matemáticas interactivas y divertidas